
As it turns out we can be more specific if we use z-score tables. In Example 1 we were able to determine that Frank’s score is better than at least 84% of the population but it does not rank in the top 2.5% of the population. c) This student scored better than only 0.15% of the class (or 99.85% of the class scored higher than this student). c) Using the 68-95-99.7 Rule, how does the student’s test score compare to the rest of the class? Show answerĪ) z-score = -3 b) This z-score is exactly 3 standard deviations less than the mean score of 76%. b) Intrepret the meaning of this z-score. We must do the same when calculating a z-score.Ĭonsider a chemistry class and a set of test scores with an average of 76% and a standard deviation of 7%.
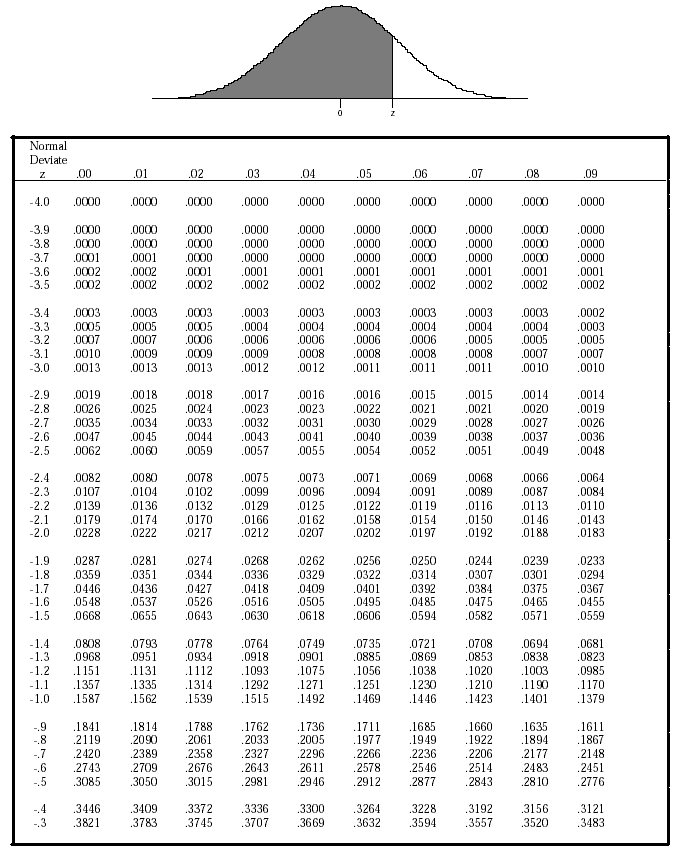
We have seen that when calculating standard deviation we must consider whether we are working with the entire population or a sample of the population. Perhaps we wish to determine the percentage of students whose test scores lie between 70% to 85%. We can also use z-scores to determine the percent of the data values that will lie between any two data values. Converting the 55% to a z-score will provide the student with a sense of where their score lies with respect to the rest of the class. The average score is 76% and one student receives a score of 55%. Consider a chemistry class with a set of test scores that is normally distributed. Z-scores can be used in situations with a normal distribution.


A z-score converts a data value and standardizes it so that we are able to determine how many standard deviations a specific data value will lie above or below the mean. The calculation does not appear so straightforward but as it turns out we can use a z-score for situations such as this. This calculation was possible since $49,000 was exactly one standard deviation away from the mean.Ĭonsider a salary which does not lie exactly one, two or three standard deviations from the mean, such as $38,500. In turn, using the 68-95-99.7 Rule we can determine that a salary of $49,000 is higher than 84% of the other salaries for this segment of the economy. With this information we are able to determine that a salary of $49,000 lies exactly one standard deviation above the mean since $45,000 + $4000 = $49, 000. Acertain segment of the economy has a normally distributed salary, with a mean salary of $45,000 and a standard deviation of $4000. Reconsider an example from the previous section. When a data set is normally distributed we can use a standardized score, called the z-score, to determine the number of standard deviations that a data value is from the mean. Approximately 99.7% of the data items fall within three standard deviations of the mean.Approximately 95% (95.44%) of the data items fall within two standard deviations of the mean.Approximately 68% (68.26%) of the data items fall within one standard deviation of the mean.

Refer to Figure 2 for the visual representation of the 68 – 95 – 99.7 Rule. We have seen that the standard deviation plays an important role in the normal distribution. The area under the curve represents 100% (or 1.00) of the data (or population) and the mean score is 0. The normal curve, also called a bell-shaped curve, is represented in Figure 1.
Negative z score table how to#
This section will explore how to determine this.Ĭonsider the normal curve which is an idealized representation of a normally distributed population. As an example, a student who has written a college entrance exam may want to know where they placed in comparison to all other students. We will shift gears and explore how to determine where a specific data value lies in relation to all other values. When a set of data values is normally distributed, the 68-95-99.7 Rule can be used to determine the percentage of values that lie one, two or three standard deviations from the mean. Solve applications using z-score tables.By the end of this section it is expected that you will be able to:


 0 kommentar(er)
0 kommentar(er)
